Type II supernova

A type II supernova belongs to a sub-category of cataclysmic variable star known as a core-collapse supernova, which results from the internal collapse and violent explosion of a massive star. The presence of hydrogen in its spectrum is what distinguishes a type II supernova from other classes of supernova explosions. A star must have at least 9 times the mass of the Sun in order to undergo this type of core-collapse.[1]
Massive stars generate energy by the nuclear fusion of elements. Unlike the Sun, these stars possess the mass needed to fuse elements that have an atomic mass greater than hydrogen and helium. The star evolves to accommodate the fusion of these accumulating, higher mass elements, until finally a core of iron is produced. However, the nuclear fusion of iron produces no net energy to sustain the star, so the core becomes an inert mass that is supported only by the degeneracy pressure of electrons. This pressure is created when any further compression of the star would require electrons to occupy the same energy state, a condition that is not possible for this type of particle. (See the Pauli exclusion principle.)
When the mass of the iron core exceeds 1.44 solar masses (the Chandrasekhar limit), an implosion ensues. The rapidly shrinking core heats up, causing rapid nuclear reactions that result in the formation of neutrons and neutrinos from the reversed beta-decay process. The collapse is halted by neutron degeneracy this time, causing the implosion to bounce outward. The energy of this expanding shock wave is sufficient to detach the surrounding stellar material, forming a supernova explosion.[2]
There exist several categories of Type II supernova explosions, which are categorized based on the resulting light curve—a graph of luminosity versus time—following the explosion. Type II-L supernovae show a steady (Linear) decline of the light curve following the explosion, whereas Type II-P display a period of slower decline (a Plateau) in their light curve followed by a normal decay. Type Ib and Ic supernovae are a type of core-collapse supernova for a massive star that has shed its outer envelope of hydrogen and (for Type Ic) helium. As a result they appear to be lacking in these elements.
Contents |
Formation
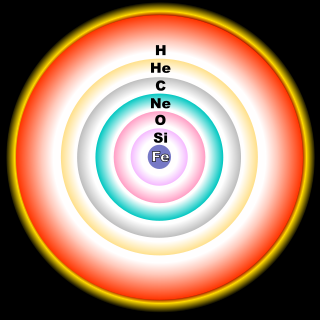
Stars far more massive than the sun evolve in more complex ways. In the core of the sun, hydrogen is fused into helium, releasing thermal energy which heats the sun's core and provides pressure which supports the sun's layers against collapse (see hydrostatic equilibrium). The helium produced in the core accumulates there since temperatures in the core are not yet high enough to cause it to fuse. Eventually, as the hydrogen at the core is exhausted, fusion starts to slow down and gravity causes the core to contract. This contraction raises the temperature high enough to initiate a shorter phase of helium fusion, which accounts for less than 10% of the star's total lifetime. In stars with less than eight solar masses, the carbon produced by helium fusion does not fuse, and the star gradually cools to become a white dwarf.[3][4] White dwarf stars, if they have a near companion, may then become Type Ia supernovae.
A much larger star, however, is massive enough to create temperatures and pressures needed to cause the carbon in the core to begin to fuse once the star contracts at the end of the helium-burning stage. The cores of these massive stars become layered like onions as progressively heavier atomic nuclei build up at the center, with an outermost layer of hydrogen gas, surrounding a layer of hydrogen fusing into helium, surrounding a layer of helium fusing into carbon (via the triple-alpha process), surrounding layers that fuse to progressively heavier elements. As a star this massive evolves, it undergoes repeated stages where fusion in the core stops, and the core collapses until the pressure and temperature is sufficient to begin the next stage of fusion, reigniting to halt collapse.[3][4]
-
Core-burning nuclear fusion stages for a 25-solar mass star Process Main fuel Main products 25 M☉ star[5] Temperature
(Kelvin)Density
(g/cm3)Duration hydrogen burning hydrogen helium 7×107 10 107 years triple-alpha process helium carbon, oxygen 2×108 2000 106 years carbon burning process carbon Ne, Na, Mg, Al 8×108 106 103 years neon burning process neon O, Mg 1.6×109 107 3 years oxygen burning process oxygen Si, S, Ar, Ca 1.8×109 107 0.3 years silicon burning process silicon nickel (decays into iron) 2.5×109 108 5 days
Core collapse
The factor limiting this process is the amount of energy that is released through fusion, which is dependent on the binding energy that holds together these atomic nuclei. Each additional step produces progressively heavier nuclei, which release progressively less energy when fusing. This continues until nickel-56 is produced (which decays radioactively into cobalt-56 and then iron-56 over the course of a few months). As iron and nickel have the highest binding energy per nucleon of all the elements,[6] energy cannot be produced at the core by fusion, and a nickel-iron core grows.[4][7] This core is under huge gravitational pressure. As there is no fusion to further raise the star's temperature to support it against collapse, it is supported only by degeneracy pressure of electrons. In this state, matter is so dense that further compaction would require electrons to occupy the same energy states. However, this is forbidden for identical fermion particles (such as the electron)—a phenomenon called the Pauli exclusion principle.
When the core's mass exceeds the Chandrasekhar limit, degeneracy pressure can no longer support it, and catastrophic collapse ensues.[8] The outer part of the core reaches velocities of up to 70,000 km/s (23% of the speed of light) as it collapses toward the center of the star.[9] The rapidly shrinking core heats up, producing high-energy gamma rays that decompose iron nuclei into helium nuclei and free neutrons (via photodisintegration). As the core's density increases, it becomes energetically favorable for electrons and protons to merge (via inverse beta decay), producing neutrons and elementary particles called neutrinos. Because neutrinos rarely interact with normal matter they can escape from the core, carrying away energy and further accelerating the collapse, which proceeds over a timescale of milliseconds. As the core detaches from the outer layers of the star, some of these neutrinos are absorbed by the star's outer layers, beginning the supernova explosion.[10]
For Type II supernovae, the collapse is eventually halted by short-range repulsive neutron-neutron interactions (mediated by the strong force), as well as by degeneracy pressure of neutrons, at a density comparable to that of an atomic nucleus. Once collapse stops, the infalling matter rebounds, producing a shock wave that propagates outward. The energy from this shock dissociates heavy elements within the core. This reduces the energy of the shock, which can stall the explosion within the outer core.[11]
The core collapse phase is so dense and energetic that only neutrinos are able to escape. As the protons and electrons combine to form neutrons by means of electron capture, an electron neutrino is produced. In a typical Type II supernova, the newly formed neutron core has an initial temperature of about 100 billion kelvin; 105 times the temperature of the sun's core. Much of this thermal energy must be shed for a stable neutron star to form (otherwise the neutrons would "boil away"), and this is accomplished by a further release of neutrinos.[12] These 'thermal' neutrinos form as neutrino-antineutrino pairs of all flavors, and total several times the number of electron-capture neutrinos.[13] The two neutrino production mechanisms convert the gravitational potential energy of the collapse into a ten second neutrino burst, releasing about 1046 joules (100 foes).[14]
Through a process that is not clearly understood, about 1044 joules (1 foe) is reabsorbed by the stalled shock, producing an explosion.[a][11] The neutrinos generated by a supernova were actually observed in the case of Supernova 1987A, leading astronomers to conclude that the core collapse picture is basically correct. The water-based Kamiokande II and IMB instruments detected antineutrinos of thermal origin,[12] while the gallium-71-based Baksan instrument detected neutrinos (lepton number = 1) of either thermal or electron-capture origin.

When the progenitor star is below about 20 solar masses (depending on the strength of the explosion and the amount of material that falls back), the degenerate remnant of a core collapse is a neutron star.[9] Above this mass the remnant collapses to form a black hole.[4][15] The theoretical limiting mass for this type of core collapse scenario is about 40–50 solar masses. Above that mass, a star is believed to collapse directly into a black hole without forming a supernova explosion,[16] although uncertainties in models of supernova collapse make calculation of these limits uncertain.
Theoretical models
The Standard Model of particle physics is a theory which describes three of the four known fundamental interactions between the elementary particles that make up all matter. This theory allows predictions to be made about how particles will interact under many conditions. The energy per particle in a supernova is typically one to one hundred and fifty picojoules (tens to hundreds of MeV).[17] The per-particle energy involved in a supernova is small enough that the predictions gained from the Standard Model of particle physics are likely to be basically correct. But the high densities may require corrections to the Standard Model.[18] In particular, Earth-based particle accelerators can produce particle interactions which are of much higher energy than are found in supernovae,[19] but these experiments involve individual particles interacting with individual particles, and it is likely that the high densities within the supernova will produce novel effects. The interactions between neutrinos and the other particles in the supernova take place with the weak nuclear force, which is believed to be well understood. However, the interactions between the protons and neutrons involve the strong nuclear force, which is much less well understood.[20]
The major unsolved problem with Type II supernovae is that it is not understood how the burst of neutrinos transfers its energy to the rest of the star producing the shock wave which causes the star to explode. From the above discussion, only one percent of the energy needs to be transferred to produce an explosion, but explaining how that one percent of transfer occurs has proven very difficult, even though the particle interactions involved are believed to be well understood. In the 1990s, one model for doing this involved convective overturn, which suggests that convection, either from neutrinos from below, or infalling matter from above, completes the process of destroying the progenitor star. Heavier elements than iron are formed during this explosion by neutron capture, and from the pressure of the neutrinos pressing into the boundary of the "neutrinosphere", seeding the surrounding space with a cloud of gas and dust which is richer in heavy elements than the material from which the star originally formed.[21]
Neutrino physics, which is modeled by the Standard Model, is crucial to the understanding of this process.[18] The other crucial area of investigation is the hydrodynamics of the plasma that makes up the dying star; how it behaves during the core collapse determines when and how the "shock wave" forms and when and how it "stalls" and is reenergized.[22] Computer models have been very successful at calculating the behavior of Type II supernovae once the shock has been formed. By ignoring the first second of the explosion, and assuming that an explosion is started, astrophysicists have been able to make detailed predictions about the elements produced by the supernova and of the expected light curve from the supernova.[23][24][25]
Light curves

When the spectrum of a Type II supernovae is examined, it normally displays Balmer absorption lines—the characteristic frequencies where hydrogen atoms absorbs energy. The presence of these lines are used to distinguish this category of supernova from a Type Ia supernova.
When the luminosity of a Type II supernova is plotted over a period of time, it shows a characteristic rise to a peak brightness followed by a decline. These light curves have an average decay rate of 0.008 magnitudes per day; much lower than the decay rate for Type Ia supernovae. Type II are sub-divided into two classes, depending on the shape of the light curve. The light curve for a Type II-L supernova shows a steady (linear) decline following the peak brightness. By contrast, the light curve of a Type II-P supernova has a distinctive flat stretch (called a plateau) during the decline; representing a period where the luminosity decays at a slower rate. The net luminosity decay rate is lower, at 0.0075 magnitudes per day for Type II-P, compared to 0.012 magnitudes per day for Type II-L.[26]
The difference in the shape of the light curves is believed to be caused, in the case of Type II-L supernovae, by the expulsion of most of the hydrogen envelope of the progenitor star.[26] The plateau phase in Type II-P supernovae is due to a change in the opacity of the exterior layer. The shock wave ionizes the hydrogen in the outer envelope—stripping the electron from the hydrogen atom—resulting in a significant increase in the opacity. This prevents photons from the inner parts of the explosion from escaping. Once the hydrogen cools sufficiently to recombine, the outer layer becomes transparent.[27]
Type IIn supernovae
The "n" denotes narrow, which indicates the presence of intermediate or very narrow width H emission lines in the spectra. In the intermediate width case, the ejecta from the explosion may be interacting strongly with gas around the star - the circumstellar medium. [28][29] SN 2005gl is one example of Type IIn; SN 2006gy, an extremely energetic supernova, may be another example.[30]
Type IIb supernovae
A type IIb supernova has a weak hydrogen line in its initial spectrum, which is why it is classified as a type II. After the initial peak in its light curve there is a second peak that has a spectrum which more closely resembles a type Ib supernova. The progenitor could have been a giant star which lost most of its hydrogen envelope due to interactions with a companion in a binary system, leaving behind the core that consisted almost entirely of helium.[31] As the ejecta of a Type IIb expands, the hydrogen layer quickly becomes more transparent and reveals the deeper layers.[32] The classic example of a type IIb supernova is Supernova 1993J,[33][34] while another example is Cassiopeia A.[35]
Hypernovae (collapsars)
The core collapse of sufficiently massive stars may not be halted. Degeneracy pressure and repulsive neutron-neutron interactions can only support a neutron star whose mass does not exceed the Tolman-Oppenheimer-Volkoff limit of very roughly 4 solar masses.[36] Above this limit, the core collapses to directly form a black hole,[16] perhaps producing a (still theoretical) hypernova explosion. In the proposed hypernova mechanism (known as a collapsar) two extremely energetic jets of plasma are emitted from the star's rotational poles at nearly light speed. These jets emit intense gamma rays, and are one of many candidate explanations for gamma ray bursts.[37]
See also
- History of supernova observation
- Supernova nucleosynthesis
- Supernova remnant
References
- ↑ Gilmore, Gerry (2004). "The Short Spectacular Life of a Superstar". Science 304 (5697): 1915–1916. doi:10.1126/science.1100370. PMID 15218132. http://www.sciencemag.org/cgi/content/full/sci;304/5679/1915. Retrieved 2007-05-01.
- ↑ Staff (2006-09-07). "Introduction to Supernova Remnants". NASA Goddard/SAO. http://heasarc.gsfc.nasa.gov/docs/objects/snrs/snrstext.html. Retrieved 2007-05-01.
- ↑ 3.0 3.1 Richmond, Michael. "Late stages of evolution for low-mass stars". Rochester Institute of Technology. http://spiff.rit.edu/classes/phys230/lectures/planneb/planneb.html. Retrieved 2006-08-04.
- ↑ 4.0 4.1 4.2 4.3 Hinshaw, Gary (2006-08-23). "The Life and Death of Stars". NASA Wilkinson Microwave Anisotropy Probe (WMAP) Mission. http://map.gsfc.nasa.gov/m_uni/uni_101stars.html. Retrieved 2006-09-01.
- ↑ Woosley, S.; Janka, H.-T. (2006-01-12). "The Physics of Core-Collapse Supernovae". Nature Physics 1 (3): 147–154. doi:10.1038/nphys172. http://adsabs.harvard.edu/abs/2006astro.ph..1261W. Retrieved 2008-10-18.
- ↑ Fewell, M. P. (1995). "The atomic nuclide with the highest mean binding energy". American Journal of Physics 63 (7): 653–658. doi:10.1119/1.17828. http://adsabs.harvard.edu/abs/1995AmJPh..63..653F. Retrieved 2007-02-01.
- ↑ Fleurot, Fabrice. "Evolution of Massive Stars". Laurentian University. http://nu.phys.laurentian.ca/~fleurot/evolution/. Retrieved 2007-08-13.
- ↑ Lieb, E. H.; Yau, H.-T. (1987). "A rigorous examination of the Chandrasekhar theory of stellar collapse". Astrophysical Journal 323 (1): 140–144. doi:10.1086/165813. http://adsabs.harvard.edu/abs/1987ApJ...323..140L. Retrieved 2007-02-01.
- ↑ 9.0 9.1 Fryer, C. L.; New, K. C. B. (2006-01-24). "Gravitational Waves from Gravitational Collapse". Max Planck Institute for Gravitational Physics. http://relativity.livingreviews.org/Articles/lrr-2003-2/. Retrieved 2006-12-14.
- ↑ Hayakawa, Takehito, Hayakawa, T.;; Iwamoto, N.; Kajino, T.; Shizuma, T.; Umeda, H.; Nomoto, K. (2006). "Principle of Universality of Gamma-Process Nucleosynthesis in Core-Collapse Supernova Explosions". The Astrophysical Journal 648: L47–L50. doi:10.1086/507703.
- ↑ 11.0 11.1 Fryer, C. L.; New, K. B. C. (2006-01-24). "Gravitational Waves from Gravitational Collapse, section 3.1". Los Alamos National Laboratory. http://relativity.livingreviews.org/open?pubNo=lrr-2003-2&page=articlesu6.html. Retrieved 2006-12-09.
- ↑ 12.0 12.1 Mann, Alfred K. (1997). Shadow of a star: The neutrino story of Supernova 1987A. New York: W. H. Freeman. p. 122. ISBN 0716730979. http://www.whfreeman.com/GeneralReaders/book.asp?disc=TRAD&id_product=1058001008&@id_course=1058000240.
- ↑ Gribbin, John R.; Gribbin, Mary (2000). Stardust: Supernovae and Life - The Cosmic Connection. New Haven: Yale University Press. p. 173. ISBN 9780300090970. http://yalepress.yale.edu/yupbooks/book.asp?isbn=9780300090970.
- ↑ Barwick, S.; Beacom, J. et al. (2004-10-29). "APS Neutrino Study: Report of the Neutrino Astrophysics and Cosmology Working Group" (PDF). American Physical Society. http://www.aps.org/policy/reports/multidivisional/neutrino/upload/Neutrino_Astrophysics_and_Cosmology_Working_Group.pdf. Retrieved 2006-12-12.
- ↑ Michael, Chris L. (2003). "Black Hole Formation from Stellar Collapse". Classical and Quantum Gravity 20 (10): S73–S80. doi:10.1088/0264-9381/20/10/309. http://adsabs.harvard.edu/abs/2003CQGra..20S..73F. Retrieved 2007-02-01.
- ↑ 16.0 16.1 Fryer, Chris L. (1999). "Mass Limits For Black Hole Formation". The Astrophysical Journal 522 (1): 413–418. doi:10.1086/307647. http://adsabs.harvard.edu/abs/1999ApJ...522..413F. Retrieved 2007-02-01.
- ↑ Izzard, R. G.; Ramirez-Ruiz, E.; Tout, C. A. (2004). "Formation rates of core-collapse supernovae and gamma-ray bursts". Monthly Notices of the Royal Astronomical Society 348 (4): 1215. doi:10.1111/j.1365-2966.2004.07436.x.
- ↑ 18.0 18.1 Rampp, M.; Buras, R.; Janka, H.-Th.; Raffelt, G. (February 11–16, 2002). "Core-collapse supernova simulations: Variations of the input physics". Proceedings of the 11th Workshop on "Nuclear Astrophysics". Ringberg Castle, Tegernsee, Germany. pp. 119–125. http://adsabs.harvard.edu/abs/2002nuas.conf..119R. Retrieved 2006-12-14.
- ↑ The OPAL Collaboration; Ackerstaff, K. et al. (1998). "Tests of the Standard Model and Constraints on New Physics from Measurements of Fermion-pair Production at 189 GeV at LEP.". [Submitted to] The European Physical Journal C 2: 441–472. doi:10.1007/s100529800851. http://publish.edpsciences.com/articles/epjc/abs/1998/05/epjc851/epjc851.html. Retrieved 2007-03-18.
- ↑ Staff (2004-10-05). "The Nobel Prize in Physics 2004". Nobel Foundation. http://nobelprize.org/nobel_prizes/physics/laureates/2004/public.html. Retrieved 2007-05-30.
- ↑ Stover, Dawn (2006). "Life In A Bubble". Popular Science 269 (6): 16.
- ↑ Janka, H.-Th.; Langanke, K.; Marek, A.; Martinez-Pinedo, G.; Mueller, B. (2006). "Theory of Core-Collapse Supernovae". Bethe Centennial Volume of Physics Reports [submitted]. http://arxiv.org/abs/astro-ph/0612072. Retrieved 2007-02-01.
- ↑ Blinnikov, S.I.; Röpke, F. K.; Sorokina, E. I.; Gieseler, M.; Reinecke, M.; Travaglio, C.; Hillebrandt, W.; Stritzinger, M. (2006). "Theoretical light curves for deflagration models of type Ia supernova". Astronomy and Astrophysics 453 (1): 229–240. doi:10.1051/0004-6361:20054594. http://adsabs.harvard.edu/abs/2006astro.ph..3036B. Retrieved 2007-02-01.
- ↑ Young, Timothy R. (2004). "A Parameter Study of Type II Supernova Light Curves Using 6 M He Cores". The Astrophysical Journal 617 (2): 1233–1250. doi:10.1086/425675. http://www.journals.uchicago.edu/doi/full/10.1086/425675. Retrieved 2008-09-17.
- ↑ Heger, A.; Rauscher, T.; Hoffman, R. D.; Woosley, S. E. (September 4–7, 2000). "Nucleosynthesis in Massive Stars Using Extended Adaptive Nuclear Reaction Networks". AIP Conference Proceedings. 561. Tours, France: American Institute of Physics. pp. 44. ISBN 1-56396-996-3. http://adsabs.harvard.edu/abs/2001tsnp.symp...44H. Retrieved 2006-12-13.
- ↑ 26.0 26.1 Doggett, J. B.; Branch, D. (1985). "A Comparative Study of Supernova Light Curves". Astronomical Journal 90: 2303–2311. doi:10.1086/113934. http://adsabs.harvard.edu/abs/1985AJ.....90.2303D. Retrieved 2007-02-01.
- ↑ "Type II Supernova Light Curves". Swinburne University of Technology. http://cosmos.swin.edu.au/lookup.html?e=typeiisupernovalightcurves. Retrieved 2007-03-17.
- ↑ doi:10.1146/annurev.astro.35.1.309
This citation will be automatically completed in the next few minutes. You can jump the queue or expand by hand - ↑ Pastorello, A.; Turatto, M.; Benetti, S.; Cappellaro, E.; Danziger, I. J.; Mazzali, P. A.; Patat, F.; Filippenko, A. V.; Schlegel, D. J.; Matheson, T. (2002). "The type IIn supernova 1995G: interaction with the circumstellar medium". Monthly Notices of the Royal Astronomical Society 333 (1): 27–38. doi:10.1046/j.1365-8711.2002.05366.x. http://adsabs.harvard.edu/abs/2002MNRAS.333...27P. Retrieved 2007-02-01.
- ↑ A bot will complete this citation soon. Click here to jump the queue arΧiv:10.1088/0004-637X/709/2/856.
- ↑ Utrobin, V. P. (1996). "Nonthermal ionization and excitation in Type IIb supernova 1993J". Astronomy and Astrophysics 306: 219–231. http://adsabs.harvard.edu/abs/1996A&A...306..219U. Retrieved 2007-02-01.
- ↑ Utrobin, V. P. (1996). "Nonthermal ionization and excitation in Type IIb supernova 1993J". Astronomy and Astrophysics 306: 219–231. http://adsabs.harvard.edu/abs/1996A&A...306..219U. Retrieved 2007-02-01.
- ↑ doi:10.1038/364507a0
This citation will be automatically completed in the next few minutes. You can jump the queue or expand by hand - ↑ doi:10.1088/2041-8205/711/1/L40
This citation will be automatically completed in the next few minutes. You can jump the queue or expand by hand - ↑ doi:10.1126/science.1155788
This citation will be automatically completed in the next few minutes. You can jump the queue or expand by hand - ↑ Bombaci, I. (1996). "The maximum mass of a neutron star". Astronomy and Astrophysics 305: 871–877. http://adsabs.harvard.edu/abs/1996A&A...305..871B. Retrieved 2007-02-01.
- ↑ "Cosmological Gamma-Ray Bursts and Hypernovae Conclusively Linked". European Organisation for Astronomical Research in the Southern Hemisphere (ESO). 2003-06-18. http://www.eso.org/outreach/press-rel/pr-2003/pr-16-03.html. Retrieved 2006-10-30.
|
|||||||||||||||||||||||||||||